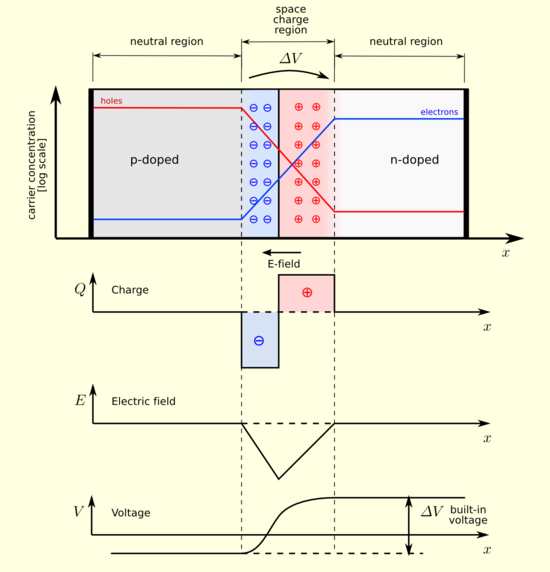
PN접합의 전류 특성을 알아보겠습니다.
현실에서는 이런 경우 PN 다이오드라고 부르는 경우가 많지요.
우선 이상적인(Ideal) PN접합 다이오드의 전류 특성 그래프는 다음과 같습니다.
Forward bias에서는 지수적으로(Exponential) 증가하고, Reverse bias에서는 미미한 전류만 있습니다.
수식으로는 다음과 같습니다.
PN 다이오드에서 전류의 원인 크게 두 가지입니다.
농도 차이에 의한 캐리어의 확산.(Diffusion)
필드에 의한 캐리어의 이동.(Drift)
이 중에서 PN 다이오드에서 우세한 것은 캐리어 확산에 의한 전류입니다.
(가정으로 인해) PN접합에서 필드가 존재하는 부분은 공핍영역뿐인데, 공핍영역에서는 캐리어가 없지요.
즉, neutral 영역에서의 캐리어 확산이 전류의 주 요인입니다.
neutral 영역에서 캐리어가 확산되기위해서는 농도 차이가 있어야하는데, majority 캐리어는 농도가 너무 높기때문에 공간에 따른 (유의미한) 농도 차이가 존재하지 않습니다.
minority 캐리어만이 공간에 따른 농도 차이를 갖고 있지요.즉, PN 다이오드에서 전류가 흐르는 원리는 'minority 캐리어의 농도차이에 의한 확산' 입니다.
minority 캐리어의 농도차이에 의한 확산 전류를 구함으로써 전체 전류를 계산합니다.
이 내용을 기본으로 두고 위 수식을 유도해보겠습니다.
이를 위해서는 몇 가지 가정이 필요합니다.
(괜히 ideal이 아니지요.)
1. 공핍영역 근사. (Depletion layer approxination)
SCR과 neutral 영역의 경계가 분명하게 존재한다고 가정합니다. 전편에서의 Space charge 분포와 같은 형태를 말하는겁니다.
2. 캐리어 분포에 맥스웰-볼츠만 근사 적용.
3. Low-level Injection
excess 캐리어 농도가 Majority 캐리어 농도보다 매우 작은 상태.
4. 전자, 홀, 총 전류는 모두 PN접합 다이오드 내에서 연속 상태.
전류를 계산하기위해서는 각 영역에서의 캐리어 분포를 알아야겠지요.
전류는 캐리어의 흐름이니까요.
전편에서 구한 Built-in voltage 식에서 시작합니다.
여기서 Perfect Ionization이라는 가정이 들어갑니다.
도핑된 불순물이 100% 이온화된다는 것. (모든 불순물이 전자와 홀을 만든다는 것.)
이제까지 계산하면서 공공연히 쓰이던 가정으로 아마 학부과정에서 계속 적용될겁니다.
실제로는 이온화도 비율이 있어서 실제로는 일부 불순물은 캐리어를 만들지 않습니다.
학부과정에서는 드물게 이 비율을 수치화해서 계산에 적용하기도 합니다.
nn0 : n타입에서의 전자 농도.
np0 : p타입에서의 전자 농도.
이 가정을 적용하면 다음의 식이 나옵니다.
p타입에서의 전자 농도는 n타입에서의 전자 농도와 관계되어 있습니다.
즉, 한 쪽의 minority 캐리어 농도가 다른 쪽의 majority 캐리어 농도와 연관되어 있다는겁니다.
여기서 forward bias 상태를 적용해보겠습니다.
(Reverse bias에서는 계산할 전류도 없으니까.)
이렇게 전자 농도 분포가 나왔습니다.
np, nn 처럼 0이 없어진건 forward bias 상태가 열평형 상태가 아니기때문입니다.
이 과정을 홀에도 적용해보면 마찬가지로 홀 농도 분포가 나옵니다.
pn0 : n타입에서의 홀 농도.
pp0 : p타입에서의 홀 농도.
앞서 PN 다이오드의 전류와 관련된 것이 minority 캐리어라고 했습니다.
우리의 관심은 minority 캐리어 농도 분포인 것이지요.
위 식에서 minority 캐리어는 pn0, np0 입니다.
excess 캐리어 식을 사용합니다.
우리가 계산할 neutral 영역에서 E-field 는 없고(E=0) 캐리어가 생성되지 않습니다. (g=0)
그리고 steady state이니 우항도 0 입니다.
steady state에서 시간에 대한 변화량은 0 이지요.
EHP 재결합이 0 이 아닌건 쉽게 생각할 수 있습니다.
n타입에서 p타입으로 확산된 전자는 당연히 p타입에 철철 넘치는 홀과 재결합할겁니다.
방향은 반대지만 홀도 마찬가지겠지요.
이런 조건을 대입하면 아래 식으로 정리됩니다.
L은 캐리어가 재결합할 때까지 이동하는 평균거리입니다.
2계 미분방정식입니다.
이걸 풀기위해서는 경계조건(boundary condition)이 필요합니다.
앞서 계산한 것과 PN 다이오드 전 영역에서 전류가 연속적이라는 가정이 경계조건이 됩니다.
(경계조건)
윗줄은 SCR 경계에서의 minority 캐리어 농도.
아래줄은 PN 다이오드 양 끝에서의 minority 캐리어 농도입니다.
SCR 경계에서 멀어질수록 재결합으로 minority 캐리어 농도가 낮아지다가 열평형상태에서의 minority 캐리어 농도로 수렴합니다.
경계조건으로 2계 미분방정식을 풀어보면 다음과 같은 식이 나옵니다.
이 식을 그래프로 표현하면 다음과 같습니다.
minority 캐리어가 확산되어 농도가 낮은 영역에 진입한 뒤 재결합하면서 exponential 하게 감소합니다.
농도차이가 존재하니 확산에 의한 전류가 존재하겠지요.
Diffusion current 식에 minority 캐리어 식을 대입해서 Diffusion current를 구합니다.
전자에 의한 전류와 홀에 의한 전류를 합치면 전체 전류가 되지요.
그래프로 나타내면 다음과 같습니다.
J는 전류밀도니까 일반적인 전류식으로 표현하면 다음과 같습니다.
PN 다이오드 길이가 L보다 작다면 재결합으로 모든 excess 캐리어가 사라질 수가 없습니다.
이 경우를 Short diode라고 하면서 설명하는 경우도 있는데 수식만 간단히 보겠습니다.
(p+ - n one sided junction. n타입 neutral 영역이 Lp보다 짧은 경우.)
(일반 case)
하지만 비현실적이니까 Ideal 이라고 하는거지요.
non-ideal 효과가 발생합니다.
- Temperature effect
온도가 올라가면 ni가 증가하고 Js가 증가합니다.
실리콘에서 온도가 10도 상승하면 전압이 17.3mV 증가한 효과가 나타난다고 합니다.
- Serise Resistance (rs)
이상적인 조건에서 PN 다이오드의 전압 강하는 SCR에서만 발생한다고 가정합니다.
하지만 neutral 영역도 저항성분이 있고 전압강하가 일어납니다.
전류가 작을 때는 무시할 수 있는 수준이지만 전류가 커지면 무시할 수 없어집니다.
전압강하는 전류의 크기에 비례하니까요.(V=Ir)
Forward bias 전압이 커질수록(=전류가 커질수록) rs의 효과나 나타나면서 전류 증가가 감소합니다.
아래 그래프처럼요.
- High-level Injection
전압이 커지면 확산되는 캐리어가 늘어나고 그 농도가 도핑농도에 근접하는 경우가 발생합니다.
excess 캐리어가 증가하는 것이고 이게 high-level injection.
Minority 캐리어인 excess 캐리어가 Majority 캐리어에 근접하게되면 재결합으로인해 Majoirty 캐리어 수가 변화하는 상황이 발생합니다.
앞서 Majority 캐리어가 일정하다고 가정했지만 Forward bias 초기에나 먹히던 것이고, Forward bias가 심화된 상태에서는 그 가정이 먹히지 않게 됩니다.
neutral 영역의 캐리어 수가 줄어드니 전류가 감소하고 이는 곧 저항이 커지는 것이지요.
- Reverse bias generation current
SCR 내에서 EHP가 생성되지 않는다고 가정했지만 실제는 EHP가 생성됩니다.
생성된 EHP는 SCR 내의 E-field에 의해 전자는 n타입쪽으로, 홀은 p타입쪽으로 가속됩니다.
전류가 발생하는 것이지요.
Reverse bias에서 Depletion width가 크고 E-field가 강하기때문에 generation current 강합니다.
수식은 이렇습니다.
- Forward bias recombination current
Forward bias에서 캐리어는 SCR을 통과합니다. (전류가 흐르니까.)
Ideal 상태에서는 SCR에서 유효 재결합이 없다고 가정했지만, 저런 조건에서 재결합이 없을리가 없지요.
캐리어가 SCR에 들어갈 때, 재결합으로 줄어든 캐리어양까지 고려해서 추가적으로 들어갑니다.
(캐리어 분포는 연속적이어야하니까.)
PN 다이오드 전체로 봤을 때 Ideal 전류보다 큰 전류가 흐르게 됩니다.
이 추가적인 전류를 recombination current 라고 합니다.
유도과정이 있지만 다 생략하고 결론만 보면 식은 이렇습니다.
Forward bias 초기에는 재결합전류가 우세하지만, 특정 지점부터 확산전류가 우세합니다.
그리고 거기서 Forward bias 심화되면 Serise resistance, high-level injection 효과로 전류 증가 정도가 감소합니다.
이를 종합한 그래프가 아래 그래프의 Forward bias 영역.
(적절한 그래프 자료를 찾기 어려우니 각 그래프에서 필요한 부분만 봅시다.)
마지막으로 Breakdown을 보지요.
개념만 간단히 보겠습니다.
본래대라면 Reverse bias 상태에서 전류가 흐를 수 없지만, Reverse bias가 심화되면서 이것이 깨어지고 급격히 전류가 흐르는겁니다.
기본적으로 breakdown이 발생하면 절연이 파괴된 것으로 다이오드를 사용할 수 없다고 봐야합니다.
그렇기때문에 Breakdown voltage 범위 내에서 사용합니다.
- Avalanche breakdown
일반적인 breakdown입니다.
Reverse bias가 심화되면 SCR내의 E-field가 강해집니다.
SCR에 유입된 캐리어는 필드에 의해 높은 에너지를 얻게 되는데, 이 캐리어가 SCR내의 다른 원자와 충돌하면 EHP를 발생시킵니다. (Impact ionization)
발생한 EHP는 다시 필드에 의해 가속되고 다시 원자와 충돌하는데, 이 과정이 반복됩니다.
캐리어가 기하급수적으로 증가합니다.
그래서 아발란체. (아발란체는 눈사태, 산사태를 뜻하지요.)
- Zener breakdown
에너지 준위 상태에 따른 전자의 터널링이 원인입니다.
본래대로라면 전자는 p타입에서 컨덕션 밴드 준위까지 에너지를 얻어 올라간 다음에 컨덕션 밴드상에서 n타입으로 이동해야합니다.
하지만 제너 다이오드처럼 도핑농도가 높고 Reverse bias가 심화되면 n타입의 컨덕션 밴드 준위가 p타입의 베일런스 밴드 준위보다 낮게되고, p타입의 전자가 n타입으로 바로 이동해버릴 수 있습니다.
에너지 장벽을 넘지않고 통과해 버린다고해서 터널링. (Tunneling)
Avalanche breakdown의 의도치않은 결과인데 반해, Zener breakdown는 의도되는 경우가 많습니다.
Breakdown 전압을 조절할 수 있는데 이를 이용하여 정전압 정류 기능을 할 수 있게 만든 것이지요.
Ideal 전류부터 Breakdown까지를 포함하는 다이오드의 전류 특성이 모두 나타나있는게 일반적으로 불 수 있는 아래와 같은 다이오드 전류 곡선인겁니다.
- 일부 이미지 출처
Donald A. Neamen, Semiconductor physics and devices 3th edition,McGraw-Hill, 2003
-
아... 힘들다. 뭐가 이렇게 내용이 많냐.
'반도체 강좌' 카테고리의 다른 글
| 삼성 3D V-NAND에 대한 잡설. (2013.08.31 update) (51) | 2013.08.19 |
|---|---|
| 반도체 강좌. (6) PN접합 (PN junction) 수식편. (21) | 2013.04.15 |
| 반도체 강좌. (5) PN접합 (PN junction) 개념편. (183) | 2013.04.14 |
| 낸드플래시(Nand Flash)에 대해 알아봅시다. (113) | 2013.04.10 |
| 반도체 강좌. (4) Nonequilibrium Excess Carriers (48) | 2013.01.05 |
































댓글